Az egyiptomi matematikai ismeretekről szóló tudásunk egyik forrása a Rhind-papirusz. Feltehetőleg i.e. 1700 körül keletkezett, de a benne szereplő ismeretek minden valószínűség szerint sokkal régebbiek. Íme az egyiptomi matematika néhány jellegzetessége: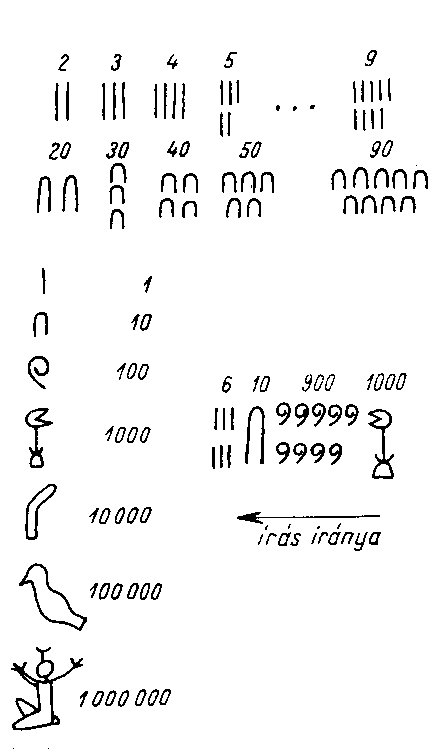

Az egyiptomiak tízes számrendszert használtak. Külön számjegyük volt tíz minden hatványának jelölésére, tehát 1-re, 10-re, 100-ra, stb. (lásd az ábrát). Az ábra alapján azt is nyilvánvaló, hogy milliós nagyságrendű számokkal is dolgoztak. A megfelelő jelek ismételt leírásával jelölték az egyéb számokat, tehát pl. a 7 leírásához az 1 jelét írták le hétszer, nem is rögzített elrendezésben. Az írás jobbról balra történt és először a nagy helyiértékeket írták le, tehát ezek a számok jobb végén találhatók.

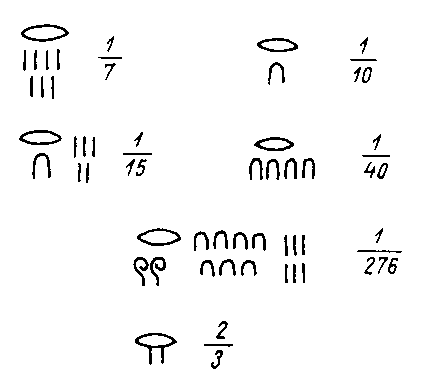
Ismerték a közönséges törteket. Ezek előállításában az egész számok reciprok értékei, tehát az 1 számlálójú törtek) fontos szerepet játszottak. Táblázataik voltak arra, hogy az egyéb törteket hogy lehet ilyen reciprokok összegeként előállítani. Ismerték pl. az alábbi előállítási módokat:

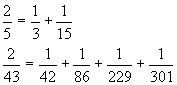
Az egész számok reciprokaként előállítható törtek leírásánál a nevezőként szolgáló szám fölé a “rész” jelét írták (lásd az ábrát). A nem ilyen alakú törtek közül csak a 2/3-nak van külön jele.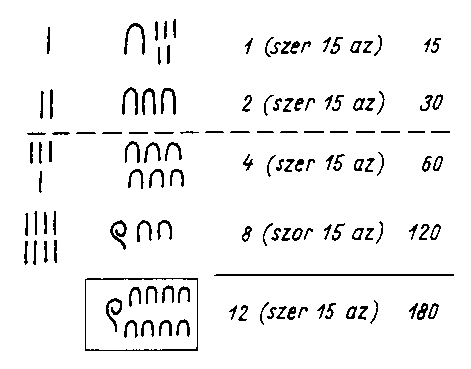

Az egyiptomiak tudtak szorozni és osztani is. A szorzandót mindig megduplázták (tehát 2 hatványaival szorozták), majd megnézték hogy mely 2-hatványokból állítható elő összeadással a szorzó (tehát gyakorlatilag előállították annak kettes számrendszerbeli alakját), majd a megfelelő hatványokhoz tartozó rész-szorzatokat összeadták. Az ábrán látható példa a 12·15 kiszámítása: 12·15=4·15+8·15. A duplicatio még a középkori Európában is szokásos számolási mód volt. Az egyiptomiak az osztást is erre a szorzásra vezették vissza: az osztót rendre megszorozták 2 hatványaival (tehát mindig duplázták), majd megnézték, hogy az osztandó hogy állítható elő ezen szorzatok összegeként. Az előállításhoz szükséges szorzatokban szereplő 2-hatványok összege kiadja a hányadost. Például a 45:5 művelet elvégzéséhez szükséges rész-szorzatok: 1·5=5, 2·5=10, 2·10=4·5=20, 2·20=8·5=40. Miután 45=40+5=8·5+1·5, ezért a hányados 8+1=9. Mint látható, már az egyiptomiak jól definiált számítási eljárást, algoritmust használtak. Az egyiptomi matematika csúcsteljesítménye a moszkvai papiruszon található: egy csonka gúla térfogatának kiszámítása (a geometria azonban nem tartozik ezen jegyzet anyagához).