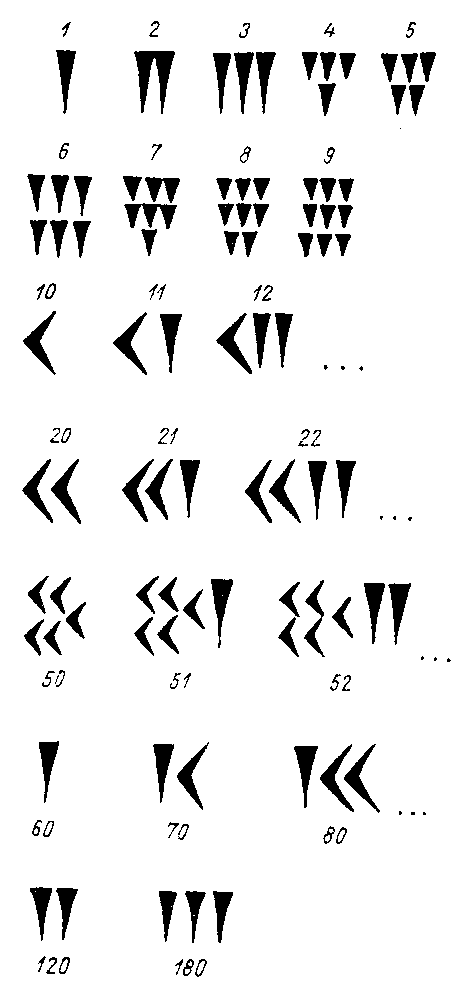
A babiloniak két legnagyobb, máig élő hozzájárulása a matematikához a 60-as számrendszer és a helyiérték bevezetése. A babiloniak nádpálcával puha agyagtáblákba írtak, majd azt kiégették. A pálca alakja okozza az ékírás jellegzetes formáját. A bibiloniak is az első kilenc számjegyet megfelelő számú vonással jelölték. A 10-re külön jelük volt, annak ismétlésével írták le a 20-at, 30-at, 40-et és 50-et (lásd az ábrát). A 60 jelölésére újból az 1-es jelét használták (helyiérték!). Így tehát 60-as számrendszerben dolgoztak, de nem volt 60 különböző számjegyük, ahogy azt az ember elsőre elvárná. A babiloniak nem használták a nullát, így aztán leírva pl. az 1 és a 60 ugyanúgy nézett ki. Csak a szövegkörnyezetből lehetett következtetni rá, hogy pontosan melyikről van szó.

Az 1-nél kisebb helyiértékeket is használták, “hatvanados” törteket írtak. Így maradt fent a értéke
1·60⁰+24·60^-1+51·60^-2+10·60^-3 alakban, 4 tizedesjegy pontossággal (1,4142):

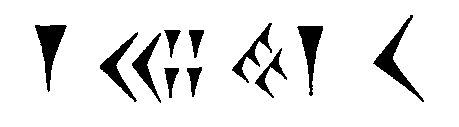
A gyökvonás elvégzésére egyébként a numerikus matematikában ma is használt iterációs eljárást alkalmazták: legyen a₀ a első, tetszőleges közelítése (akár 1-et is vehetünk), minden további közelítést pedig az előzőből az

képlet szerint számolták. Ez az eljárás meglepően gyorsan konvergál: ha pl. a₀=1-ből indulunk, akkor a₁=1,5 és a₂=1,415...

A hatvanas számrendszer és a helyiértékes számábrázolás aztán elkerült Alexandriába, ahol Ptolemaiosz is ezt használta. Ő már a nulla jelölésére üres helyet hagyott ki a számok leírásakor, de a 0 mint számjegy még nem jelent meg. Ehhez a hindu kultúra kellett.